Лекция: Отрывок из учебника по теории систем и системному анализу

Лекция: Отрывок из учебника по теории систем и системному анализу

ре­сурсов на основе учета возможного вклада (определяемого мето­да экспертной

оценки) различных отраслей и научных направле­ний в решение какого-либо круга

задач.

Метод SEER (System for Event Evaluation and Review систе­ма оценок и

обзора событий) предусматривает всего два тура оценки. В каждом туре

привлекается различный состав экспер­тов. Эксперты первого тура - специалисты

промышленности, эк­сперты второго тура - наиболее квалифицированные

специалис­ты из органов, принимающих решения, и специалисты в области

естественных и технических наук. Эксперт каждого тура не воз­вращается к

рассмотрению своих ответов за исключением тех случаев, когда его ответ выпадает

из некоторого интервала, в котором находится большинство оценок (например,

интервала, в котором находится 90 % всех оценок).

2.4.5. МЕТОДЫ ТИПА ДЕРЕВА ЦЕЛЕЙ

Идея метода впервые была предложена Черчменом в связи с проблемами принятия

решений в промышленности. Термин «де­рево целей» подразумевает использование

иерархической струк­туры, полученной путем разделения общей цели на подцели,

а

128

Глава 2

Основы оценки сложных систем

129

их, в свою очередь, на более детальные составляющие (новые подцели, функции и

т.д.)- Как правило, этот термин использует­ся для структур, имеющих отношение

строгого порядка, но ме­тод дерева целей используется иногда и применительно

к «сла­бым» иерархиям, в которых одна и та же вершина нижележащего уровня

может быть одновременно подчинена двум или несколь­ким вершинам вышележащего

уровня.

Разновидностью методов дерева целей и Дельфи является ме­тод PA TTERN

(Planning Assistance Through Technical Evaluation of Relevance Numbers помощь

планированию посредством от­носительных показателей технической оценки),

разработанный для повышения эффективности процессов принятия решений в области

долгосрочной научно-технической ориентации крупной промышленной фирмы.

Сущность метода PATTERN заключается в следующем. Ис­ходя из сформулированных

целей потребителей продукции фир­мы на прогнозируемый период осуществляется

развертывание дерева целей. Для каждого уровня дерева целей вводится ряд

кри­териев. С помощью экспертной оценки определяются веса крите­риев и

коэффициенты значимости, характеризующие важность вклада целей в обеспечение

критериев. Значимость некоторой цели определяется коэффициентом связи,

представляющим сум­му произведений всех критериев на соответствующие

коэффици­енты значимости. Общий коэффициент связи некоторой цели

(от­носительно достижения цели высшего уровня) определяется пу­тем

перемножения соответствующих коэффициентов связи в направлении вершины

дерева.

2.4.6. МОРФОЛОГИЧЕСКИЕ МЕТОДЫ

Основная идея морфологических методов систематически находить все мыслимые

варианты решения проблемы или реа­лизации системы путем комбинирования

выделенных элемен­тов или их признаков. В систематизированном виде

морфоло­гический подход разработан и применен впервые швейцарским астрономом

Ф. Цвикки и долгое время был известен как метод Цвикки.

Цвикки предложил три метода морфологического исследо­вания:

1. Метод систематического покрытия поля (МСПП), основан­

ный на выделении так называемых опорных пунктов знания в

любой исследуемой области и использовании для заполнения поля

некоторых сформулированных принципов мышления.

2. Метод отрицания и конструирования (МОК), заключаю­

щийся в том, что на пути конструктивного прогресса стоят дог­

мы и компромиссные ограничения, которые есть смысл отрицать,

и следовательно, сформулировав некоторые предложения, полез­

но заменить их затем на противоположные и использовать при

проведении анализа.

3. Метод морфологического ящика (ММЯ), нашедший наи­

более широкое распространение. Идея ММЯ состоит в том, что­

бы определить все мыслимые параметры, от которых может за­

висеть решение проблемы, представить их в виде матриц-строк,

а затем определить в этом морфологическом матрице-ящике все

возможные сочетания параметров по одному из каждой строки.

Полученные таким образом варианты могут снова подвергаться

оценке и анализу в целях выбора наилучшего. Морфологический

ящик может быть не только двумерным.

Построение и исследование по методу морфологического ящика проводится в пять

этапов.

Этап 1. Точная формулировка поставленной проблемы.

Этап 2. Выделение показателей Pt, от которых зависит ре­шение

проблемы. По мнению Ф. Цвикки, при наличии точной формулировки проблемы

выделение показателей происходит ав­томатически.

Этап 3. Сопоставление показателю Pf его значений ;? А и

све­дение этих значений в таблицу, которую Цвикки и называет мор­фологическим

ящиком.

Набор значений различных показателей (по одному значению из каждой строки)

представляет собой возможный вариант ре­шения данной проблемы (например,

вариант {р1,, р22, ... , pk

n}, обозначенный на рис. 2.7). Такие наборы называются вари­антами

решения или просто вариантами. Общее число ва­риантов, содержащихся в

морфологической таблице, равно N = К\К2 ... Кп,

где Kt (i = 1, 2, ... , и) - число значений /-го пока­зателя.

д—20

24

Глава 1

ского пространства обычно рассматривается временной интер­вал (0, °°).

Аксиома 2. Пространство состояний Z содержит не менее двух элементов. Эта

аксиома отражает естественное представле­ние о том, что сложная система может

находиться в разных со­стояниях.

Аксиома 3. Система обладает свойством функциональной эмерджентности .

Эмерджентностъ (целостность) - это такое свойство систе­мы S,

которое принципиально не сводится к сумме свойств эле­ментов, составляющих

систему, и не выводится из них:

т

1

где yt - i-я характеристика системы S; т - общее количество характеристик.

При таком рассмотрении система является совокупностью моделей и, главное,

отражает семантику предметной области в отличие от неинтерпретированных частных

математических мо­делей. Другими словами, система - это совокупность

взаимосвя­занных элементов, обладающая интегративными свойствами

(эмерджентностью), а также способ отображения реальных объектов.

В рамках изучаемой дисциплины под сложной кибернетичес­кой системой

понимается реальный объект с управлением и его отображение в сознании

исследователя как совокупность моде­лей, адекватная решаемой задаче.

123 КЛАССИФИКАЦИЯ СИСТЕМ

Системы принято подразделять на физические и абстрактные, динамические и

статические, простые и сложные, естественные и искусственные, с управлением и

без управления, непрерывные и дискретные, детерминированные и стохастические,

открытые и замкнутые.

Основы системного анализа

Деление систем на физические и абстрактные позволяет раз­личать реальные

системы (объекты, явления, процессы) и систе­мы, являющиеся определенными

отображениями (моделями) ре­альных объектов.

Для реальной системы может быть построено множество сис­тем - моделей,

различаемых по цели моделирования, по требуе­мой степени детализации и по

другим признакам.

Например, реальная ЛВС, с точки зрения системного адми­нистратора, -

совокупность программного, математического, информационного,

лингвистического, технического и других видов обеспечения, с точки зрения

противника, - совокупность объектов, подлежащих разведке, подавлению

(блокированию), уничтожению, с точки зрения технического обслуживания, -

со­вокупность исправных и неисправных средств.

Деление систем на простые и сложные (большие) подчерки­вает, что в

системном анализе рассматриваются не любые, а имен­но сложные системы большого

масштаба. При этом выделяют структурную и функциональную (вычислительную)

сложность.

Общепризнанной границы, разделяющей простые, большие и сложные системы, нет.

Однако условно будем считать, что слож­ные системы характеризуются тремя

основными признаками: свойством робастности, наличием неоднородных связей и

эмер­джентностью.

Во-первых, сложные системы обладают свойством робастно­сти -

способностью сохранять частичную работоспособность (эффективность) при отказе

отдельных элементов или подсистем. Оно объясняется функциональной избыточностью

сложной сис­темы и проявляется в изменении степени деградации выполняе­мых

функций, зависящей от глубины возмущающих воздействий. Простая система может

находиться не более чем в двух состоя­ниях: полной работоспособности

(исправном) и полного отказа (неисправном).

Во-вторых, в составе сложных систем кроме значительного количества элементов

присутствуют многочисленные и разные по типу (неоднородные) связи между

элементами. Основными типа­ми считаются следующие виды связей: структурные (в

том числе иерархические), функциональные, каузальные (причинно-след­ственные,

отношения истинности), информационные, простран­ственно-временные. По этому

признаку будем отличать сложные

26

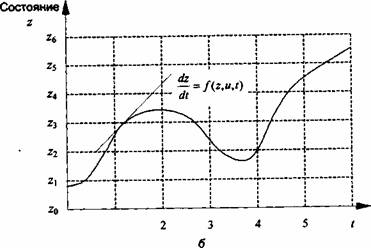
Глава 1

системы от больших систем, представляющих совокупность од­нородных элементов,

объединенных связью одного типа.

В-третьих, сложные системы обладают свойством, которое отсутствует у любой из

составляющих ее частей. Это интегратив-ность (целостность), или

эмерджентность. Другими словами, от­дельное рассмотрение каждого элемента не

дает полного пред­ставления о сложной системе в целом. Эмерджентность может

достигаться за счет обратных связей, играющих важнейшую роль в управлении

сложной системой.

Считается, что структурная сложность системы должна быть пропорциональна объему

информации, необходимой для ее опи­сания (снятия неопределенности). В этом

случае общее количе­ство информации о системе S, в которой априорная

вероятность появленияу'-ro свойства равна р(у), определяется известным

со­отношением для количества информации

I(Y) = -Ip(yj)log2p(yj). (1.6)

Это энтропийный подход к дескриптивной (описательной) сложности.

Одним из способов описания такой сложности является оцен­ка числа элементов,

входящих в систему (переменных, состояний, компонентов), и разнообразия

взаимозависимостей между ними.

В общей теории систем утверждается, что не существует сис­тем обработки данных,

которые могли бы обработать более чем 2-10547 бит в секунду на грамм

своей массы. При этом компью­терная система, имеющая массу, равную массе Земли,

за период, равный примерно возрасту Земли, может обработать порядка 10593

бит информации (предел Бреммермана). Задачи, требующие обработки более чем 10

593 бит, называются трансвычислитель­ными. В практическом плане

это означает, что, например, пол­ный анализ системы из 110 переменных, каждая

из которых мо­жет принимать 7 разных значений, является трансвычислитель­ной

задачей.

Для оценки сложности функционирования систем применя­ется алгоритмический

подход. Он основан на определении ресур­сов (время счета или используемая

память), используемых в сис­теме при решении некоторого класса задач.

Например, если фун­кция времени вычислений является полиномиальной функцией

от входных данных, то мы имеем дело с полиномиальным по вре-

Ф-

ч)

0

Ч

^

1с

Основы системного анализа

мени, или «легким» алгоритмом. В случае экспоненциального по времени

алгоритма говорят о его «сложности». Алгоритмическая сложность изучается в

теории NP-полных задач.

Сложные системы допустимо делить на искусственные и ес­тественные (природные).

Искусственные системы, как правило, отличаются от природ­ных наличием

определенных целей функционирования (назначе­нием) и наличием управления.

Рассмотрим еще один важный признак классификации сис­тем. Принято считать, что

система с управлением, имеющая не­тривиальный входной сигнал x(t) и

выходной сигнал y(t), может рассматриваться как преобразователь

информации, перерабаты­вающий поток информации (исходные данные) x(t) в

поток ин­формации (решение по управлению) y(t).

В соответствии с типом значений x(t), y(t), z(t) и t системы

де­лятся на дискретные и непрерывные.

Такое деление проводится в целях выбора математического аппарата

моделирования. Так, теория обыкновенных дифферен­циальных уравнений и

уравнений в частных производных позво­ляет исследовать динамические системы с

непрерывной перемен­ной (ДСНП). С другой стороны, современная техника создает

антропогенные динамические системы с дискретными события­ми (ДСДС), не

поддающиеся такому описанию. Изменения со­стояния этих систем происходят не

непрерывно, а в дискретные моменты времени, по принципу «от события к

событию». Мате­матические (аналитические) модели заменяются на имитацион­ные,

дискретно-событийные: модели массового обслуживания, сети Петри, цепи Маркова

и др.

Примеры фазовых траекторий ДСДС и ДСНП показаны на рис. 1.3, а, б.

Для ДСДС траектория является кусочно-постоянной и фор­мируется

последовательностью событий и. Последовательность отрезков постоянства

отражает последовательность состояний z системы, а длительность каждого

отрезка отражает время пре­бывания системы в соответствующем состоянии.

Под состоя­нием при этом понимается «физическое» состояние (например, число

сообщений, ожидающих передачи в каждом узле обра­ботки). Состояния принимают

значения из дискретного мно­жества.

28

Основы системного анализа

29

Состояние j,

z

"3

25 24 23

«5

«2

F

t4 ts

h '3 a

0 1

to

Рис. 1.З. Типичные примеры фазовых траекторий ДСДС(а)иДСНП(б)

Таким образом, траектория описывается последовательно­стью из двух чисел

(состояния и времени пребывания в нем). Сле­дует подчеркнуть, что термин

«дискретный» отличается от ши­роко используемого прилагательного «цифровой»,

поскольку последнее означает лишь то, что анализ задачи ведется не в тер­минах

вещественной числовой переменной, а численными мето­дами. Траектория ДСНП,

состояниями которой являются точки пространства R", постоянно

изменяется и, вообще говоря, разви­вается на основе непрерывных входных

воздействий. Здесь под состоянием понимается «математическое» состояние в том

смыс­ле, что оно включает в себя информацию к данному моменту вре­мени (кроме

внешних воздействий), которая необходима для од­нозначного определения

дальнейшего поведения системы. Ма­тематическое определение включает в себя и

физическое определение, но не наоборот.

Для перехода от детерминированной к стохастической систе­ме

достаточно в правые части соотношений (1.4) и (1.5) добавить в качестве

аргументов функционалов случайную функцию p(t), принимающую значения на

непрерывном или дискретном мно­жестве действительных чисел.

Следует иметь в виду, что в отличие от математики для сис­темного анализа, как и

для кибернетики, характерен конструк­тивный подход к изучаемым объектам. Это

требует обеспечения корректности задания системы, под которой

понимается возмож­ность фактического вычисления выходного сигнала y(t)

(с той или иной степенью точности) для всех / > 0 при задании начального

состояния системы z(0) и входного сигнала x(t) для всех it

. Поэто­му при изучении сложных систем приходится переходить к ко­нечным

аппроксимациям.

Системы с нетривиальным входным сигналом x(t), источни­ком которого

нельзя управлять (непосредственно наблюдать), или системы, в которых

неоднозначность их реакции нельзя объяс­нить разницей в состояниях, называются

открытыми.

Признаком, по которому можно определить открытую систе­му, служит наличие

взаимодействия с внешней средой. Взаимо­действие порождает проблему

«предсказуемости» значений вы­ходных сигналов и, как следствие, - трудности

описания откры­тых систем.

30

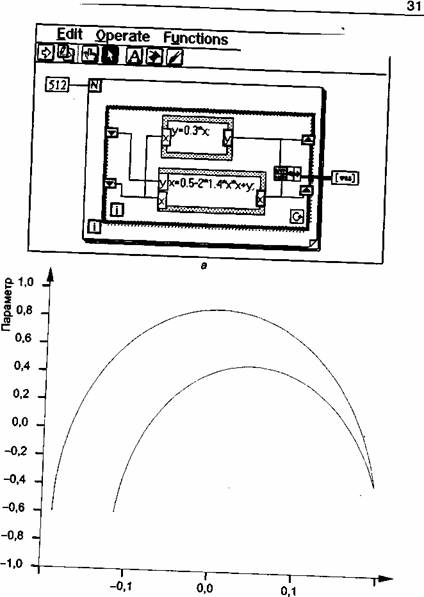
Глава 1

Примером трудностей описания является понятие «странный аттрактор» -

специфическое свойство некоторых сложных сис­тем. Простейший аттрактор,

называемый математиками непод­вижной точкой, представляет собой такой вид

равновесия, кото­рый характерен для состояния устойчивых систем после

кратков­ременного возмущения (состояние покоя емкости с водой после

встряхивания). Второй вид аттрактора - предельный цикл маят­ника. Все

разновидности предельного цикла предсказуемы. Тре­тья разновидность

называется странным аттрактором. Обнару­жено много систем, имеющих встроенные

в них источники нару­шений, которые не могут быть заранее предсказаны

(погода, место остановки шарика в рулетке). В экспериментах наблюдали за

краном, из которого нерегулярно капали капли, хотя проме­жутки должны быть

регулярными и предсказуемыми, так как вен­тиль зафиксирован и поток воды

постоянен.

Математическим примером странного аттрактора является аттрактор Хенона -

система уравнений, смоделированная в Lab VIEW (рис. 1.4, а, б).

Понятие открытости систем конкретизируется в каждой пред­метной области.

Например, в области информатики открытыми информационными системами

называются программно-аппарат­ные комплексы, которым присущи следующие

свойства:

• переносимость (мобильность) - программное обеспечение

(ПО) может быть легко перенесено на различные аппаратные

платформы и в различные операционные среды;

• стандартность - программное обеспечение соответствует

опубликованному стандарту независимо от конкретного разра­

ботчика ПО;

• наращиваемость возможностей - включение новых про­

граммных и технических средств, не предусмотренных в перво­

начальном варианте;

• совместимость - возможность взаимодействовать с други­

ми комплексами на основе развитых интерфейсов для обмена

данными с прикладными задачами в других системах.

Примером открытой среды является модель OSE (Open System Environment),

предложенная комитетом IEEE POSIX. На основе этой модели Национальный

институт стандартов и технологии США выпустил документ «Application

Portability Profile (APP). The U.S. Government's Open System Environment

Profile OSE/1

WindowsIextHe'P

-0,2

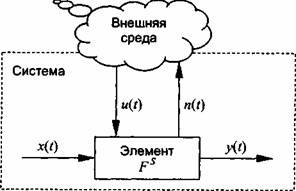
Основы системного анализа

0,2 Состояние

рис. 1.4. Аттрактор Хенона: - программная модель; б -

поведение в пространстве состояний

32

33

Version 2.0», который определяет рекомендуемые спецификации в области

информационных технологий, гарантирующие мобиль­ность системного и

прикладного программного обеспечения.

В отличие от открытых замкнутые (закрытые) системы изо­лированы от среды

- не оставляют свободных входных компо­нентов ни у одного из своих элементов.

Все реакции замкнутой системы однозначно объясняются изменением ее состояний.

Век­тор входного сигнала x(t) в замкнутых системах имеет нулевое число

компонентов и не может нести никакой информации. Замкнутые системы в строгом

смысле слова не должны иметь не только входа, но и выхода. Однако даже в этом

случае их можно интерпретировать как генераторы информации, рассматривая

из­менение их внутреннего состояния во времени. Примером физи­ческой замкнутой

системы является локальная сеть для обработ­ки конфиденциальной информации.

Основным противоречием, которое приходится разрешать в замкнутых системах,

является проблема возрастания энтропии. Согласно второму закону термодинамики

по мере движения зам­кнутой системы к состоянию равновесия она стремится к

мак­симальной энтропии (дезорганизации), соответствующей мини­мальной

информации. Открытые системы могут изменить это стремление к максимальной

энтропии, получая внешнюю по от­ношению к системе свободную энергию, и этим

поддерживают организацию.

закон функционирования Fs, и в зависимости от целей

модели­рования входной сигнал x(t) может быть разделен на три

под­множества:

• неуправляемых входных сигналов xt е X, I = 1, ... , kx, пре­

образуемых рассматриваемым элементом;

• воздействий внешней среды «v e N, v = 1, ... , kn, представ­

ляющих шум, помехи;

• управляющих сигналов (событий) ит е U, т = 1........... ku,

появление которых приводит к переводу элемента из одного со­стояния в другое.

Иными словами, элемент - это неделимая наименьшая функци­ональная часть

исследуемой системы, включающая < х, п, и, у, f^> и

представляемая как «черный ящик» (рис. 1.5). Функциональную модель элемента

будем представлять как y(t) = Fs(x, п, и, t).

Входные сигналы, воздействия внешней среды и управляю­щие сигналы являются

независимыми переменными. При стро­гом подходе изменение любой из независимых

переменных вле­чет за собой изменение состояния элемента системы. Поэтому в

дальнейшем будем обобщенно обозначать эти сигналы как x(t), a

функциональную модель элемента - как y(t) = Fs(x(t)), если

это не затрудняет анализ системы.

Выходной сигнал y(t), в свою очередь, представляют совокуп­ностью

характеристик элемента j>. e Y,j = l,...,k

1.2.4.

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ СИСТЕМНОГО АНАЛИЗА

Для оперирования основными понятиями системного анали­за будем придерживаться

следующих словесно-интуитивных или формальных определений.

Элемент - некоторый объект (материальный, энергетичес­кий,

информационный), обладающий рядом важных свойств и реализующий в системе

определенный закон функционирования F8, внутренняя структура

которого не рассматривается.

Формальное описание элемента системы совпадает с описа­нием подмодели Ч* .

Однако функционалы g и / заменяются на

Рис. 1.5. Элемент системы как «черный ящик»

3-20

34

Глава 1

Основы системного анализа

35

Под средой понимается множество объектов S 'вне данно­го

элемента (системы), которые оказывают влияние на элемент (систему) и сами

находятся под воздействием элемента (системы),

Правильное разграничение исследуемого реального объекта и среды является

необходимым этапом системного анализа. Часто в системном анализе выделяют

понятие «суперсистема» - часть внеш­ней среды, для которой исследуемая

система является элементом.

Подсистема - часть системы, выделенная по определенно­му признаку,

обладающая некоторой самостоятельностью и до­пускающая разложение на элементы в

рамках данного рассмот­рения.

Система может быть разделена на элементы не сразу, а после­довательным

расчленением на подсистемы - совокупности эле­ментов. Такое расчленение, как

правило, производится на осно­ве определения независимой функции, выполняемой

данной со­вокупностью элементов совместно для достижения некой частной цели,

обеспечивающей достижение общей цели системы. Подси­стема отличается от

простой группы элементов, для которой не выполняется условие целостности.

Последовательное разбиение системы в глубину приводит к иерархии подсистем,

нижним уровнем которых является элемент. Типичным примером такого разбиения

является структура Пас­каль-программы. Так, например, тело основной программы

вклю­чает модули - подсистемы первого уровня, модули включают функции и

процедуры - подсистемы второго уровня, функции и процедуры включают операнды

и операторы - элементы системы.

Характеристика -то, что отражает некоторое свойство элемента системы.

Характеристика v задается кортежем ^. = < name, {value} >, где

пате - имя 7-й характеристики, {value} - область допустимых

значений. Область допустимых значений задается перечислени­ем этих значений или

функционально, с помощью правил вычис­ления (измерения) и оценки.

Характеристики делятся на количественные и качественные в зависимости от типа

отношений на множестве их значений.

Если на множестве значений заданы метризованные отноше­ния, когда указывается не

только факт выполнения отношения p(W, у?), н° также и

степень количественного превосходства, то

характеристика является количественной. Например, размер эк­рана

(см), максимальное разрешение (пиксель) являются количе­ственными

характеристиками мониторов, поскольку существу­ют шкалы измерений этих

характеристик в сантиметрах и пиксе­лях соответственно, допускающие

упорядочение возможных значений по степени количественного превосходства:

размер эк­рана монитора у! больше, чем размер экрана монитора _у А на 3

см (аддитивное метризованное отношение) или максимальное раз­решение у/

1 выше, чем максимальное разрешение у?,в два раза

(мультипликативное метризованное отношение).

Если пространство значений не метрическое, то характерис­тика называется

качественной. Например, такая характеристика монитора, как комфортное

разрешение, хотя и измеряется в пик­селях, является качественной. Поскольку

на комфортность влия­ют мерцание, нерезкость, индивидуальные особенности

пользо­вателя и т.д., единственным отношением на шкале комфортнос­ти является

отношение эквивалентности, позволяющее различить мониторы как комфортные и

некомфортные без установления количественных предпочтений.

Количественная характеристика называется параметром.

Часто в литературе понятия «параметр» и «характеристика» отождествляются на

том основании, что все можно измерить. Но в общем случае полезно разделять

параметры и качественные характеристики, так как не всегда возможно или

целесообразно разрабатывать процедуру количественной оценки какого-либо

свойства.

Характеристики элемента являются зависимыми переменны­ми и отражают свойства

элемента. Под свойством понима­ют сторону объекта, обусловливающую его

отличие от других объектов или сходство с ними и проявляющуюся при

взаимодей­ствии с другими объектами.

Свойства задаются с использованием отношений одного из основных

математических понятий, используемых при анализе и обработке информации. На

языке отношений единым образом можно описать воздействия, свойства объектов и

связи между ними, задаваемые различными признаками. Существует несколь­ко

форм представления отношений: функциональная (в виде фун­кции, функционала,

оператора), матричная, табличная, логичес­кая, графовая, представление

сечениями, алгоритмическая (в виде словесного правила соответствия).

з-

36

Глава 1

Основы системного анализа

37

Свойства классифицируют на внешние, проявляющиеся в фор­ме выходных

характеристик yt только при взаимодействии с вне­шними

объектами, и внутренние, проявляющиеся в форме пере­менных состояния z,

при взаимодействии с внутренними элемен­тами рассматриваемой системы и

являющиеся причиной внешних свойств.

Одна из основных целей системного анализа - выявление внут­ренних свойств

системы, определяющих ее поведение.

По структуре свойства делят на простые и сложные (интег­ральные). Внешние

простые свойства доступны непосредствен­ному наблюдению, внутренние свойства

конструируются в нашем сознании логически и не доступны наблюдению.

Следует помнить о том, что свойства проявляются только при взаимодействии с

другими объектами или элементами одного объекта между собой.

По степени подробности отражения свойств выделяют гори­зонтальные

(иерархические) уровни анализа системы. По харак­теру отражаемых свойств

выделяют вертикальные уровни ана­лиза - аспекты. Этот механизм лежит в основе

утверждения о том, что для одной реальной системы можно построить множество

абстрактных систем.

При проведении системного анализа на результаты влияет фактор времени. Для

своевременного окончания работы необхо­димо правильно определить уровни и

аспекты проводимого ис­следования. При этом производится выделение

существенных для данного исследования свойств путем абстрагирования от

несу­щественных по отношению к цели анализа подробностей.

Формально свойства могут быть представлены также и в виде закона

функционирования элемента.

Законом функционирования Fs, описывающим процесс

функ­ционирования элемента системы во времени, называется зависи­мость y(t)

= Fs( x, n, и, t).

Оператор Fs преобразует независимые переменные в зависи­мые и

отражает поведение элемента (системы) во времени - про­цесс изменения

состояния элемента (системы), оцениваемый по степени достижения цели его

функционирования. Понятие пове­дения принято относить только к целенаправленным

системам и оценивать по показателям.

Цель - ситуация или область ситуаций, которая должна быть достигнута при

функционировании системы за определенный промежуток времени. Цель может

задаваться требованиями к показателям результативности, ресурсоемкости,

оперативности функционирования системы либо к траектории достижения за­данного

результата. Как правило, цель для системы определяет­ся старшей системой, а

именно той, в которой рассматриваемая система является элементом.

Показатель - характеристика, отражающая качествоу'-й системы или целевую

направленность процесса (операции), реа­лизуемого у'-й системой:

YJ = WJ(n, x, и).

Показатели делятся на частные показатели качества (или

эф­фективности) системы у>(, которые отражают /-е

существенное свойство7-й системы, и обобщенный показатель качества (или

эф­фективности) системы Y J — вектор, содержащий совокупность

свойств системы в целом. Различие между показателями качества и эффективности

состоит в том, что показатель эффективности характеризует процесс (алгоритм) и

эффект от функционирова­ния системы, а показатели качества - пригодность

системы для использования ее по назначению.

Вид отношений между элементами, который проявляется как некоторый обмен

(взаимодействие), называется связью. Как правило, в исследованиях

выделяются внутренние и внешние свя­зи. Внешние связи системы - это ее связи со

средой. Они проявля­ются в виде характерных свойств системы. Определение

внешних связей позволяет отделить систему от окружающего мира и явля­ется

необходимым начальным этапом исследования.

В ряде случаев считается достаточным исследование всей си­стемы ограничить

установлением ее закона функционирования. При этом систему отождествляют с

оператором F5 и представля­ют в виде «черного ящика». Однако

в задачах анализа обычно требуется выяснить, какими внутренними связями

обусловлива­ются интересующие исследователя свойства системы. Поэтому основным

содержанием системного анализа является определе­ние структурных,

функциональных, каузальных, информацион­ных и пространственно-временных

внутренних связей системы.

38

Глава 1

Основы системного анализа

39

Структурные связи обычно подразделяют на иерархические, сетевые, древовидные

и задают в графовой или матричной форме.

Функциональные и пространственно-временные связи зада­ют как функции,

функционалы и операторы.

Каузальные (причинно-следственные) связи описывают на языке формальной логики.

Для описания информационных связей разрабатываются ин-фологические модели.

Выделение связей разных видов наряду с выделением элемен­тов является

существенным этапом системного анализа и позво­ляет судить о сложности

рассматриваемой системы.

Важным для описания и исследования систем является поня­тие алгоритм

функционирования As, под которым по­нимается метод получения

выходных характеристик y(t) с учетом входных воздействий x(i),

управляющих воздействий u(f) и воз­действий внешней среды n(t).

По сути, алгоритм функционирования раскрывает механизм проявления внутренних

свойств системы, определяющих ее по­ведение в соответствии с законом

функционирования. Один и тот же закон функционирования элемента системы может

быть реа­лизован различными способами, т. е. с помощью множества раз­личных

алгоритмов функционирования As.

Наличие выбора алгоритмов As приводит к тому, что систе­мы с

одним и тем же законом функционирования обладают раз­ным качеством и

эффективностью процесса функционирования.

Качество - совокупность существенных свойств объекта, обусловливающих его

пригодность для использования по назна­чению. Оценка качества может

производиться по одному интег­ральному свойству, выражаемому через обобщенный

показатель качества системы.

Процессом называется совокупность состояний системы z(/0),

z(/,), ... , z(tk), упорядоченных по изменению какого-либо

параметра г, определяющего свойства системы.

Формально процесс функционирования как последователь­ная смена состояний

интерпретируется как координаты точки в А>мерном фазовом пространстве.

Причем каждой реализации процесса будет соответствовать некоторая фазовая

траектория. Совокупность всех возможных значений состояний {z}

называ­ется пространством состояний системы.

Проиллюстрировать понятие процесса можно на следующем примере. Состояние узла

связи будем характеризовать количе­ством исправных связей на коммутаторе.

Сделаем ряд измерений, при которых количество связей будет иметь разные

значения. Будет ли полученный набор значений характеризовать некото­рый

процесс? Без дополнительной информации это неизвестно. Если это упорядоченные

по времени / (параметр процесса) зна­чения, то - да. Если же значения

перемешаны, то соответствую­щий набор состояний не будет процессом.

В общем случае время в модели системы S может рассматри­ваться на

интервале моделирования (О, 7) как непрерывное, так и дискретное, т.е.

квантованное на отрезки длиной Д/ временных единиц каждый, когда T = mAt,

где т - число интервалов диск­ретизации.

Эффективность процесса - степень его приспособ­ленности к достижению цели.

Принято различать эффективность процесса, реализуемого системой, и качество

системы. Эффективность проявляется толь­ко при функционировании и зависит от

свойств самой системы, способа ее применения и от воздействий внешней среды.

К? и т ерий эффективности - обобщенный показа­тель и правило выбора

лучшей системы (лучшего решения). На­пример, Y* = max{YJ}.

Если решение выбирается по качественным характеристикам, то критерий

называется решающим правилом.

Если нас интересует не только закон функционирования, но и алгоритм реализации

этого закона, то элемент не может быть представлен в виде «черного ящика» и

должен рассматриваться как подсистема (агрегат, домен) - часть системы,

выделенная по функциональному или какому-либо другому признаку.

Описание подсистемы в целом совпадает с описанием элемен­та. Но для ее описания

дополнительно вводится понятие множе­ства внутренних (собственных)

характеристик подсистемы А,е Н, 1=1, ..., kh.

Оператор Fs преобразуется к виду y(t) = Fs (

х, п, и, h, t), a метод получения выходных характеристик кроме входных

воз­действий x(t), управляющих воздействий u(t) и воздействий

внеш­ней среды n(f) должен учитывать и собственные характеристики

подсистемы h(t).

40

Глава 1

41

Описание закона функционирования системы наряду с ана­литическим, графическим,

табличным и другими способами в ряде случаев может быть получено через

состояние системы. Состояние системы - это множество значений

характе­ристик системы в данный момент времени.

Формально состояние системы в момент времени Г0 < t* < Т

полностью определяется начальным состоянием z(/0), входными

воздействиями x(t), управляющими воздействиями u(i),

внутрен­ними параметрами h(t) и воздействиями внешней среды n(i),

ко­торые имели место за промежуток времени t* - tQ, с помощью

гло­бальных уравнений динамической системы (1.4), (1.5), преобра­зованных к

виду

Вход системы А

Вход системы "В

0.

g, t];

y(t) = g(z(t), t).

Здесь уравнение состояния по начальному состоянию z(f0) и переменным

х, и, п, h определяет вектор-функцию z(i), а уравне­ние наблюдения

по полученному значению состояний z(t) опре­деляет переменные на выходе

подсистемы y(t).

Таким образом, цепочка уравнений объекта «вход-состояния-выход» позволяет

определить характеристики подсистемы:

ХО =/Ш'0)' х, и, п, h, 0]

и под математической моделью реальной системы можно пони­мать конечное

подмножество переменных (x(t), u(t), n(i), h(t)} вместе с

математическими связями между ними и характеристи­ками y(f).

Структура - совокупность образующих систему элемен­тов и связей между

ними. Это понятие вводится для описания под­модели Ч*6. В структуре

системы существенную роль играют свя­зи. Так, изменяя связи при сохранении

элементов, можно полу­чить другую систему, обладающую новыми свойствами или

реализующую другой закон функционирования. Это наглядно видно на рис. 1 .6,

если в качестве системы рассматривать соеди­нение трех проводников, обладающих

разными сопротивлениями.

Необходимость одновременного и взаимоувязанного рассмот­рения состояний

системы и среды требует определения понятий «ситуация» и «проблема».

Выход системы А a

Выход системы В б

Рис. 1.6. Роль связей в структуре системы: а - параллельная

связь; б - последовательная связь

Ситуация - совокупность состояний системы и среды в один и тот же момент

времени.

Проблема - несоответствие между существующим и тре­буемым (целевым)

состоянием системы при данном состоянии сре­ды в рассматриваемый момент

времени.

1.3. МОДЕЛИ СЛОЖНЫХ СИСТЕМ

Под моделированием понимается процесс исследования реаль­ной системы,

включающий построение модели, изучение ее свойств и перенос полученных сведений

на моделируемую систему.

Общими функциями моделирования являются описание, объяснение и

прогнозирование поведения реальной системы.

Типовыми целями моделирования могут быть поиск опти­мальных или близких к

оптимальным решений, оценка эффектив­ности решений, определение свойств

системы (чувствительности

42

Глава 1

Основы системного анализа

43

к изменению значений характеристик и др.), установление взаи­мосвязей между

характеристиками системы, перенос информа­ции во времени. Термин «модель» имеет

весьма многочисленные трактовки. В наиболее общей формулировке мы будем

придер­живаться следующего определения модели. Модель - это объект,

который имеет сходство в некоторых отношениях с про­тотипом и служит средством

описания и/или объяснения, и/или прогнозирования поведения прототипа.

Формальное определение модели (1.1) определяет модель как изоморфизм А на Ч1.

Частные модели могут обозначаться как гомоморфизм:

Оператор / в этом обозначении указывает на способ, кото­рый позволяет

построить требуемую модель.

Важнейшим качеством модели является то, что она дает уп­рощенный образ,

отражающий не все свойства прототипа, а толь­ко те, которые существенны для

исследования.

Сложные системы характеризуются выполняемыми процес­сами (функциями),

структурой и поведением во времени. Для адек­ватного моделирования этих

аспектов в автоматизированных информационных системах различают

функциональные, инфор­мационные и поведенческие модели, пересекающиеся друг с

другом.

Функциональная модель системы описывает совокупность вы­полняемых

системой функций, характеризует морфологию сис­темы (ее построение) - состав

функциональных подсистем, их взаимосвязи.

Информационная модель отражает отношения между элемен­тами системы в виде

структур данных (состав и взаимосвязи).

Поведенческая (событийная) модель описывает информаци­онные процессы

(динамику функционирования), в ней фигуриру­ют такие категории, как состояние

системы, событие, переход из одного состояния в другое, условия перехода,

последовательность событий.

Особенно велико значение моделирования в системах, где натурные эксперименты

невозможны по целому ряду причин: сложность, большие материальные затраты,

уникальность, дли-

тельность эксперимента. Так, нельзя «провести войну в мирное время», натурные

испытания некоторых типов систем связаны с их разрушением, для

экспериментальной проверки сложных сис­тем управления требуется длительное

время и т.д.

Можно выделить три основные области применения моделей: обучение, научные

исследования, управление. При обучении с помощью моделей достигается высокая

наглядность отображе­ния различных объектов и облегчается передача знаний о

них. Это в основном модели, позволяющие описать и объяснить сис­тему. В

научных исследованиях модели служат средством полу­чения, фиксирования и

упорядочения новой информации, обес­печивая развитие теории и практики. В

управлении модели ис­пользуются для обоснования решений. Такие модели должны

обеспечить как описание, так и объяснение и предсказание пове­дения систем.

1.3.1.

КЛАССИФИКАЦИЯ ВИДОВ МОДЕЛИРОВАНИЯ СИСТЕМ

Классификация видов моделирования может быть проведена по разным основаниям.

Один из вариантов классификации при­веден на рис. 1.7.

В соответствии с классификационным признаком полноты моделирование делится на

полное, неполное и приближенное. При полном моделировании модели

идентичны объекту во вре­мени и пространстве. Для неполного

моделирования эта идентич­ность не сохраняется. В основе приближенного

моделирования лежит подобие, при котором некоторые стороны реального объекта не

моделируются совсем. Теория подобия утверждает, что абсолютное подобие возможно

лишь при замене одного объекта другим точно таким же. Поэтому при моделировании

абсолютное подобие не имеет места. Исследователи стремятся к тому, чтобы модель

хорошо отображала только исследуемый ас­пект системы. Например, для оценки

помехоустойчивости диск­ретных каналов передачи информации функциональная и

инфор­мационная модели системы могут не разрабатываться. Для дос­тижения цели

моделирования вполне достаточна событийная

Общегосударственные органы управления

Республиканские и отраслевые органы управления

Страницы: 1, 2, 3